Which Reaction Would Cause An Increase In Entropy
19.6: Gibbs Free energy Change and Equilibrium
- Folio ID
- 24319
Learning Objectives
- To know the relationship between gratis energy and the equilibrium abiding.
- The sign of the standard free free energy change Δ1000° of a chemical reaction determines whether the reaction will tend to go along in the forward or opposite direction.
- Similarly, the relative signs of ΔG° and ΔDue south° determine whether the spontaniety of a chemic reaction volition be afflicted by the temperature, and if and then, in what way.
ΔGrand is meaningful only for changes in which the temperature and pressure remain constant. These are the atmospheric condition under which near reactions are carried out in the laboratory; the system is unremarkably open to the temper (constant pressure) and we begin and cease the process at room temperature (after any oestrus nosotros have added or which is liberated past the reaction has dissipated.) The importance of the Gibbs function tin can hardly be over-stated: it serves as the single master variable that determines whether a given chemic change is thermodynamically possible. Thus if the gratuitous energy of the reactants is greater than that of the products, the entropy of the world will increase when the reaction takes place every bit written, and and so the reaction will tend to take place spontaneously. Conversely, if the free energy of the products exceeds that of the reactants, so the reaction will non take identify in the management written, but it will tend to proceed in the reverse direction.
Temperature Dependence to ΔG
In a spontaneous change, Gibbs energy e'er decreases and never increases. This of course reflects the fact that the entropy of the earth behaves in the exact opposite way (attributable to the negative sign in the TΔS term).
\[H_2O_{(l)} \rightarrow H_2O_{(due south)} \characterization{23.5.6}\]
h2o below its freezing point undergoes a decrease in its entropy, but the rut released into the surroundings more than compensates for this, so the entropy of the world increases, the free energy of the H2O diminishes, and the process proceeds spontaneously.
Annotation
In a spontaneous modify, Gibbs free energy e'er decreases and never increases.
An important consequence of the one-way downward path of the free energy is that in one case it reaches its minimum possible value, all internet change comes to a halt. This, of course, represents the land of chemical equilibrium. These relations are nicely summarized equally follows:
- ΔG < 0: reaction can spontaneously go on to the right: \[A \rightarrow B\]
- ΔG > 0: reaction tin spontaneously proceed to the left: \[A \leftarrow B\]
- ΔG = 0: the reaction is at equilibrium; the quantities of [A] and [B] will non alter
Recall the status for spontaneous change
\[ΔG = ΔH – TΔS < 0 \label{Master}\]
it is credible that the temperature dependence of ΔG depends about entirely on the entropy change associated with the process. (We say "almost" because the values of ΔH and ΔS are themselves slightly temperature dependent; both gradually increment with temperature). In particular, observe that in the above equation the sign of the entropy change determines whether the reaction becomes more or less spontaneous as the temperature is raised. For any given reaction, the sign of ΔH can also be positive or negative. This means that there are iv possibilities for the influence that temperature can have on the spontaneity of a process.
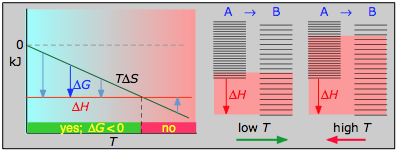
The post-obit cases generalizes these relations for the four sign-combinations of ΔH and ΔS. (Note that use of the standard ΔH° and ΔS° values in the case reactions is not strictly right here, and can yield misleading results when used more often than not.)
> 0
Nether these conditions, both the ΔH and TΔDue south terms volition be negative, so ΔG will be negative regardless of the temperature. An exothermic reaction whose entropy increases will be spontaneous at all temperatures.

Instance Reaction
\[C_{(graphite)} + O_{2(g)} \rightleftharpoons CO_{2(g)}\]
- ΔH° = –393 kJ
- ΔSouthward° = +two.9 J K–1
- ΔG° = –394 kJ at 298 K
The positive entropy alter is due mainly to the greater mass of CO2 molecules compared to those of O2.
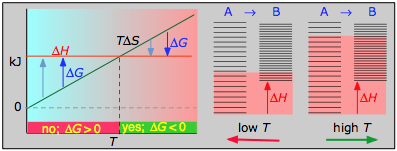
< 0
If the reaction is sufficiently exothermic it can force Δ G negative only at temperatures below which | TΔSouthward | < |Δ H |. This means that in that location is a temperature T = Δ H / Δ S at which the reaction is at equilibrium; the reaction will only continue spontaneously below this temperature. The freezing of a liquid or the condensation of a gas are the near mutual examples of this condition.
Case reaction:
\[iii H_2 + N_2 \rightleftharpoons ii NH_{iii(g)}\]
- ΔH° = –46.ii kJ
- ΔS° = –389 J G–1
- ΔG° = –16.four kJ at 298 K
The decrease in moles of gas in the Haber ammonia synthesis drives the entropy change negative, making the reaction spontaneous only at depression temperatures. Thus higher T, which speeds upwards the reaction, as well reduces its extent.
> 0
This is the reverse of the previous example; the entropy increase must overcome the handicap of an endothermic process so that TΔS > ΔH. Since the effect of the temperature is to "magnify" the influence of a positive ΔS, the process will exist spontaneous at temperatures above T = ΔH / ΔS. (Think of melting and boiling.)
Example reaction:
\[N_2O_{4(one thousand)} \rightleftharpoons 2 NO_{2(chiliad)}\]
- ΔH° = 55.3 kJ
- ΔS° = +176 J K–1
- ΔG° = +2.eight kJ at 298 Yard
Dissociation reactions are typically endothermic with positive entropy modify, and are therefore spontaneous at high temperatures.Ultimately, all molecules decompose to their atoms at sufficiently high temperatures.
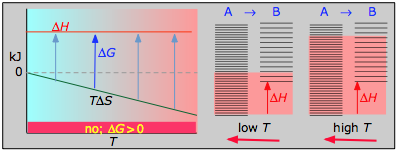
< 0
With both ΔH and ΔSouth working against it, this kind of process will not proceed spontaneously at any temperature. Substance A always has a greater number of accessible energy states, and is therefore e'er the preferred form.
Case reaction:
\[½ N_2 + O_2 \rightleftharpoons NO_{2(g)}\]
- ΔH° = 33.2 kJ
- ΔS° = –249 J K–1
- ΔChiliad° = +51.3 kJ at 298 K
This reaction is non spontaneous at any temperature, meaning that its opposite is always spontaneous. Merely because the reverse reaction is kinetically inhibited, NO2 can exist indefinitely at ordinary temperatures even though it is thermodynamically unstable.
The to a higher place cases and associated plots are the important ones; do non endeavour to memorize them, but make certain you understand and tin explain or reproduce them for a given set of ΔH and ΔS.
- Their most important differentiating features are the position of the ΔH line (above or beneath the is TΔS line), and the slope of the latter, which of course depends on the sign of ΔDue south.
- The reaction A → B will occur spontaneously only when ΔG is negative (blue arrows pointing down.)
- Attributable to the slight temperature dependence of ΔSouthward , the TΔS plots are not quite straight lines as shown here. Similarly, the lines representing ΔH are even more curved.
The other ii plots on each diagram are only for the chemistry-committed.
- Each pair of free energy-level diagrams depicts the relative spacing of the microscopic energy levels in the reactants and products equally reflected by the value of ΔS°. (The greater the entropy, the more closely-spaced are the quantized microstates.)
- The red shading indicates the range of energy levels that are attainable to the arrangement at each temperature. The spontaneous direction of the reaction will ever exist in the direction in which the red shading overlaps the greater number of free energy levels, resulting in the maximum dispersal of thermal energy.
- Notation that the vertical offsets correspond to ΔH° for the reaction.
- Never forget that it is the power of thermal free energy to spread into every bit many of these states as possible that determines the tendency of the process to accept identify. None of this is to calibration, of course!
Liquid-Vapor Equilibrium
To further understand how the diverse components of ΔG dictate whether a procedure occurs spontaneously, we now wait at a unproblematic and familiar concrete change: the conversion of liquid water to h2o vapor. If this process is carried out at 1 atm and the normal humid point of 100.00°C (373.fifteen K), we can calculate ΔG from the experimentally measured value of ΔHvap (40.657 kJ/mol). For vaporizing 1 mol of water, \(ΔH = 40,657; J\), so the procedure is highly endothermic. From the definition of ΔS, we know that for ane mol of water,
\(\Delta S_{\textrm{vap}}=\dfrac{\Delta H_{\textrm{vap}}}{T_\textrm b}=\dfrac{\textrm{40,657 J}}{\textrm{373.xv K}}=\textrm{108.96 J/K}\)
Hence there is an increment in the disorder of the system. At the normal boiling point of water,
\[\Delta G_{100^\circ\textrm C}=\Delta H_{100^\circ\textrm C}-T\Delta S_{100^\circ\textrm C}=\textrm{40,657 J}-[(\textrm{373.15 Thousand})(\textrm{108.96 J/One thousand})]=\textrm{0 J}\]
The energy required for vaporization offsets the increase in disorder of the organisation. Thus ΔG = 0, and the liquid and vapor are in equilibrium, as is true of any liquid at its boiling point under standard weather.
Now suppose we were to superheat i mol of liquid water to 110°C. The value of ΔG for the vaporization of 1 mol of h2o at 110°C, assuming that ΔH and ΔS do not modify significantly with temperature, becomes
\[\Delta G_{110^\circ\textrm C}=\Delta H-T\Delta Due south=\textrm{40,657 J}-[(\textrm{383.15 K})(\textrm{108.96 J/K})]=-\textrm{1091 J}\]
At 110°C, ΔG < 0, and vaporization is predicted to occur spontaneously and irreversibly.
We can likewise summate ΔG for the vaporization of 1 mol of water at a temperature beneath its normal humid point—for instance, 90°C—making the same assumptions:
\[\Delta G_{90^\circ\textrm C}=\Delta H-T\Delta Due south=\textrm{40,657 J}-[(\textrm{363.15 One thousand})(\textrm{108.96 J/1000})]=\textrm{1088 J}\]
At 90°C, ΔG > 0, and water does not spontaneously convert to water vapor. When using all the digits in the calculator display in conveying out our calculations, ΔG110°C = 1090 J = −ΔG90°C, as we would predict.
Nosotros can also calculate the temperature at which liquid water is in equilibrium with water vapor. Inserting the values of ΔH and ΔS into the definition of ΔG (Equation \(\ref{Main}\)), setting ΔG = 0, and solving for T,
0 J=40,657 J−T(108.96 J/K)
T=373.fifteen K
Thus ΔG = 0 at T = 373.xv Grand and 1 atm, which indicates that liquid water and water vapor are in equilibrium; this temperature is called the normal humid point of h2o. At temperatures greater than 373.15 One thousand, ΔG is negative, and water evaporates spontaneously and irreversibly. Below 373.15 1000, ΔG is positive, and water does non evaporate spontaneously. Instead, water vapor at a temperature less than 373.xv M and ane atm volition spontaneously and irreversibly condense to liquid water. Effigy \(\PageIndex{1}\) shows how the ΔH and TΔS terms vary with temperature for the vaporization of water. When the ii lines cantankerous, ΔG = 0, and ΔH = TΔS.

A similar state of affairs arises in the conversion of liquid egg white to a solid when an egg is boiled. The major component of egg white is a protein chosen albumin, which is held in a meaty, ordered construction past a large number of hydrogen bonds. Breaking them requires an input of energy (ΔH > 0), which converts the albumin to a highly disordered structure in which the molecules aggregate as a disorganized solid (ΔS > 0). At temperatures greater than 373 Thou, the TΔS term dominates, and ΔG < 0, and then the conversion of a raw egg to a hard-boiled egg is an irreversible and spontaneous process to a higher place 373 M.
Free Energy and the Equilibrium Constant
ΔOne thousand is key in determining whether or not a reaction volition have place in a given direction. It turns out, nonetheless, that it is almost never necessary to explicitly evaluate ΔG. It is far more than user-friendly to work with the equilibrium constant of a reaction, within which ΔG is "hidden". This is just as well, because for most reactions (those that take place in solutions or gas mixtures) the value of ΔG depends on the proportions of the various reaction components in the mixture; information technology is not a simple sum of the "products minus reactants" type, as is the example with ΔH.
Because ΔH° and ΔS° determine the magnitude of ΔG° and because Thou is a measure of the ratio of the concentrations of products to the concentrations of reactants, we should exist able to limited Thousand in terms of ΔG° and vice versa. ΔG is equal to the maximum amount of work a system can perform on its surround while undergoing a spontaneous change. For a reversible process that does non involve external piece of work, we can express the change in free free energy in terms of volume, force per unit area, entropy, and temperature, thereby eliminating ΔH from the equation for ΔG. The general human relationship can be shown as follow (derivation non shown):
\[ \Delta G = 5 \Delta P − S \Delta T \label{xviii.29}\]
If a reaction is carried out at constant temperature (ΔT = 0), then Equation \(\ref{eighteen.29}\) simplifies to
\[\Delta{G} = V\Delta{P} \label{xviii.xxx}\]
Nether normal conditions, the pressure dependence of free energy is not of import for solids and liquids because of their minor tooth volumes. For reactions that involve gases, even so, the effect of pressure on gratis energy is very important.
Bold ideal gas behavior, we can supplant the \(Five\) in Equation \(\ref{xviii.30}\) by nRT/P (where n is the number of moles of gas and R is the ideal gas constant) and express \(\Delta{G}\) in terms of the initial and final pressures (\(P_i\) and \(P_f\), respectively):
\[\Delta G=\left(\dfrac{nRT}{P}\correct)\Delta P=nRT\dfrac{\Delta P}{P}=nRT\ln\left(\dfrac{P_\textrm f}{P_\textrm i}\right) \label{18.31}\]
If the initial state is the standard state with Pi = 1 atm, then the change in energy of a substance when going from the standard state to any other state with a pressure P can exist written as follows:
\[G − Yard^° = nRT\ln{P}\]
This can be rearranged equally follows:
\[M = G^° + nRT\ln {P} \label{xviii.32}\]
As you will soon find, Equation \(\ref{18.32}\) allows us to relate ΔG° and Kp. Any relationship that is true for \(K_p\) must also be true for \(K\) because \(K_p\) and \(K\) are but unlike ways of expressing the equilibrium constant using different units.
Let's consider the post-obit hypothetical reaction, in which all the reactants and the products are ideal gases and the lowercase letters correspond to the stoichiometric coefficients for the various species:
\[aA+bB \rightleftharpoons cC+dD \label{18.33}\]
Because the free-energy change for a reaction is the difference between the sum of the gratuitous energies of the products and the reactants, we can write the post-obit expression for ΔG:
\[\delta{G}=\sum_m G_{products}−\sum_n G_{reactants}=(cG_C+dG_D)−(aG_A+bG_B) \label{18.34}\]
Substituting Equation \(\ref{18.32}\) for each term into Equation \(\ref{18.34}\),
\[ΔG=[(cG^o_C+cRT \ln P_C)+(dG^o_D+dRT\ln P_D)]−[(aG^o_A+aRT\ln P_A)+(bG^o_B+bRT\ln P_B)]\]
Combining terms gives the following relationship between ΔG and the reaction quotient Q:
\[\Delta Yard=\Delta G^\circ+RT \ln\left(\dfrac{P^c_\textrm CP^d_\textrm D}{P^a_\textrm AP^b_\textrm B}\right)=\Delta Thousand^\circ+RT\ln Q \label{xviii.35}\]
where ΔG° indicates that all reactants and products are in their standard states. For gases at equilibrium (\(Q = K_p\),), and as you've learned in this chapter, ΔG = 0 for a arrangement at equilibrium. Therefore, we can describe the relationship between ΔG° and Thousandp for gases as follows:
\[ 0 = ΔG° + RT\ln K_p \label{eighteen.36a}\]
\[ \color{blood-red} ΔG°= −RT\ln K_p \characterization{18.36b}\]
If the products and reactants are in their standard states and ΔG° < 0, then Chiliadp > 1, and products are favored over reactants. Conversely, if ΔG° > 0, then Kp < i, and reactants are favored over products. If ΔG° = 0, then \(K_p = 1\), and neither reactants nor products are favored: the system is at equilibrium.
Note
For a spontaneous process under standard conditions, \(K_{eq}\) and \(K_p\) are greater than 1.
Example \(\PageIndex{one}\)
Nosotros previosuly calculated that ΔG° = −32.7 kJ/mol of N2 for the reaction
\[N_{two(thousand)}+3H_{2(g)} \rightleftharpoons 2NH_{iii(one thousand)} \nonumber\]
This calculation was for the reaction nether standard weather—that is, with all gases nowadays at a partial force per unit area of ane atm and a temperature of 25°C. Calculate ΔG for the same reaction under the following nonstandard conditions:
- \(P_{\textrm N_2}\) = 2.00 atm,
- \(P_{\textrm H_2}\) = 7.00 atm,
- \(P_{\textrm{NH}_3}\) = 0.021 atm,
- and T = 100°C.
Does the reaction favor products or reactants?
Given: balanced chemic equation, partial pressure level of each species, temperature, and ΔG°
Asked for: whether products or reactants are favored
Strategy:
- Using the values given and Equation \(\ref{18.35}\), calculate Q.
- Substitute the values of ΔG° and Q into Equation \(\ref{eighteen.35}\) to obtain ΔG for the reaction under nonstandard conditions.
Solution:
A The relationship between ΔG° and ΔG nether nonstandard conditions is given in Equation \(\ref{eighteen.35}\). Substituting the partial pressures given, we tin can calculate Q:
\[Q=\dfrac{P^2_{\textrm{NH}_3}}{P_{\textrm N_2}P^3_{\textrm H_2}}=\dfrac{(0.021)^2}{(2.00)(vii.00)^three}=half dozen.4\times10^{-7} \nonumber\]
B Substituting the values of ΔG° and Q into Equation \(\ref{18.35}\),
\(\Delta G=\Delta Thousand^\circ+RT\ln Q=-32.7\textrm{ kJ}+\left[(\textrm{viii.314 J/K})(\textrm{373 One thousand})\left(\dfrac{\textrm{1 kJ}}{\textrm{1000 J}}\right)\ln(half-dozen.4\times10^{-vii})\correct]\)
\(=-32.vii\textrm{ kJ}+(-44\textrm{ kJ})\)
\(=-77\textrm{ kJ/mol of Northward}_2\)
Because ΔG < 0 and Q < 1.0, the reaction is spontaneous to the correct every bit written, so products are favored over reactants.
Exercise \(\PageIndex{1}\)
Calculate ΔG for the reaction of nitric oxide with oxygen to give nitrogen dioxide under these weather condition: T = 50°C, PNO = 0.0100 atm, \(P_{\mathrm{O_2}}\) = 0.200 atm, and \(P_{\mathrm{NO_2}}\) = 1.00 × 10−4 atm. The value of ΔG° for this reaction is −72.5 kJ/mol of Otwo. Are products or reactants favored?
Answer: −92.9 kJ/mol of O2; the reaction is spontaneous to the right as written, so products are favored.
Case \(\PageIndex{2}\)
Calculate Kp for the reaction of H2 with Due northii to give NHiii at 25°C. Every bit calculated in Instance ten, ΔG° for this reaction is −32.vii kJ/mol of Northward2.
Given: balanced chemical equation from Example 10, ΔG°, and temperature
Asked for: Kp
Strategy:
Substitute values for ΔG° and T (in kelvins) into Equation \(\ref{18.36}\) to calculate Mp, the equilibrium abiding for the formation of ammonia.
Solution
In Case x, we used tabulated values of ΔG∘ f to calculate ΔG° for this reaction (−32.7 kJ/mol of N2). For equilibrium atmospheric condition, rearranging Equation \(\ref{18.36b}\),
\(\brainstorm{marshal} \Delta Grand^\circ &=-RT\ln K_\textrm p \nonumber
\\ \dfrac{-\Delta G^\circ}{RT} &=\ln K_\textrm p \nonumber \end{align}\)
Inserting the value of ΔG° and the temperature (25°C = 298 K) into this equation,
\(\begin{align}\ln K_\textrm p &=-\dfrac{(-\textrm{32.7 kJ})(\textrm{m J/kJ})}{(\textrm{viii.314 J/Thousand})(\textrm{298 K})}=13.ii
\nonumber \\ K_\textrm p &=5.4\times10^5 \nonumber\terminate{align}\)
Thus the equilibrium constant for the formation of ammonia at room temperature is favorable. However, the rate at which the reaction occurs at room temperature is too dull to be useful.
Exercise \(\PageIndex{ii}\)
Summate Kp for the reaction of NO with O2 to give NO2 at 25°C. As calculated in the do in Example ten, ΔG° for this reaction is −70.v kJ/mol of Otwo.
Answer: 2.2 × 1012
Although Thoup is divers in terms of the partial pressures of the reactants and the products, the equilibrium constant K is divers in terms of the concentrations of the reactants and the products. We described the human relationship between the numerical magnitude of Yardp and Thousand in Affiliate 15 and showed that they are related:
\[K_p = K(RT)^{Δn} \label{xviii.37}\]
where Δn is the number of moles of gaseous product minus the number of moles of gaseous reactant. For reactions that involve but solutions, liquids, and solids, Δn = 0, so Mp = K. For all reactions that do not involve a change in the number of moles of gas present, the relationship in Equation \(\ref{eighteen.36b}\) can be written in a more full general form:
\[ΔG° = −RT \ln K \label{18.38}\]
Only when a reaction results in a cyberspace production or consumption of gases is information technology necessary to right Equation \(\ref{eighteen.38}\) for the difference betwixt Kp and Thou. Although we typically use concentrations or pressures in our equilibrium calculations, recall that equilibrium constants are more often than not expressed equally unitless numbers because of the use of activities or fugacities in precise thermodynamic work. Systems that incorporate gases at high pressures or concentrated solutions that deviate substantially from ideal behavior require the use of fugacities or activities, respectively.
Combining Equations \(\ref{18.38}\) with \(ΔG^o = ΔH^o − TΔS^o\) provides insight into how the components of ΔG° influence the magnitude of the equilibrium constant:
\[ΔG° = ΔH° − TΔS° = −RT \ln M \label{eighteen.39}\]
Equation \(\ref{eighteen.39}\) is quite powerful and connected the nature of the system under equilibrium \(Thou\) to the condition of the arrangement under standard conditions \(\Delta M^o\).; that is quite powerful. Notice that \(K\) becomes larger as ΔS° becomes more positive, indicating that the magnitude of the equilibrium constant is directly influenced past the tendency of a arrangement to motility toward maximum disorder. Moreover, K increases every bit ΔH° decreases. Thus the magnitude of the equilibrium constant is besides directly influenced by the tendency of a system to seek the lowest energy state possible.
Note
The magnitude of the equilibrium constant is directly influenced past the tendency of a system to move toward maximum entropy and seek the lowest energy state possible.
To further illustrate the relation between these two essential thermodynamic concepts, consider the observation that reactions spontaneously proceed in a direction that ultimately establishes equilibrium. As may be shown by plotting the free free energy change versus the extent of the reaction (for example, every bit reflected in the value of Q), equilibrium is established when the organisation'due south free energy is minimized (Figure \(\PageIndex{2}\)). If a system is present with reactants and products present in nonequilibrium amounts (Q ≠ K), the reaction volition proceed spontaneously in the management necessary to establish equilibrium.
Relating Grxn and Kp: https://youtu.be/T-OYNTYN__4
ΔG° and ΔG: Predicting the Direction of Chemical Change
We have seen that there is no way to mensurate accented enthalpies, although nosotros can mensurate changes in enthalpy (ΔH) during a chemical reaction. Because enthalpy is one of the components of Gibbs free energy, we are consequently unable to measure absolute free energies; we can measure only changes in costless free energy. The standard free-energy modify (ΔG°) is the alter in free energy when one substance or a set of substances in their standard states is converted to one or more other substances, likewise in their standard states. The standard free-energy change can exist calculated from the definition of free energy, if the standard enthalpy and entropy changes are known, using Equation \(\ref{Eq5}\):
\[ΔG° = ΔH° − TΔS° \label{Eq5}\]
If ΔS° and ΔH° for a reaction have the same sign, so the sign of ΔG° depends on the relative magnitudes of the ΔH° and TΔS° terms. Information technology is important to recognize that a positive value of ΔG° for a reaction does not mean that no products volition class if the reactants in their standard states are mixed; it ways only that at equilibrium the concentrations of the products will exist less than the concentrations of the reactants.
Note
A positive ΔG° ways that the equilibrium constant is less than i.
Example \(\PageIndex{3}\)
Calculate the standard complimentary-energy change (ΔG°) at 25°C for the reaction
\[H_{2(g)}+O_{2(k)} \rightleftharpoons H_2O_{2(l)} \nonumber\]
At 25°C, the standard enthalpy change (ΔH°) is −187.78 kJ/mol, and the absolute entropies of the products and reactants are:
- S°(HtwoO2) = 109.6 J/(mol•K),
- Due south°(Otwo) = 205.2 J/(mol•K), and
- S°(Htwo) = 130.7 J/(mol•K).
Is the reaction spontaneous as written?
Given: balanced chemical equation, ΔH° and S° for reactants and products
Asked for: spontaneity of reaction equally written
Strategy:
- Calculate ΔS° from the absolute tooth entropy values given.
- Utilize Equation \(\ref{Eq5}\), the calculated value of ΔS°, and other information given to calculate ΔG° for the reaction. Use the value of ΔG° to determine whether the reaction is spontaneous as written.
Solution
A To calculate ΔG° for the reaction, we need to know ΔH°, ΔS°, and T. We are given ΔH°, and we know that T = 298.15 K. We can summate ΔS° from the accented tooth entropy values provided using the "products minus reactants" dominion:
\(\begin{marshal}\Delta Southward^\circ &=South^\circ(\mathrm{H_2O_2})-[S^\circ(\mathrm{O_2})+S^\circ(\mathrm{H_2})]
\nonumber \\ &=[\mathrm{1\;mol\;H_2O_2}\times109.6\;\mathrm{J/(mol\cdot K})]
\nonumber \\ &-\left \{ [\textrm{1 mol H}_2\times130.7\;\mathrm{J/(mol\cdot K)}]+[\textrm{1 mol O}_2\times205.2\;\mathrm{J/(mol\cdot K)}] \correct \}
\nonumber \\&=-226.3\textrm{ J/K }(\textrm{per mole of }\mathrm{H_2O_2}) \end{align}\)
As nosotros might await for a reaction in which 2 mol of gas is converted to 1 mol of a much more ordered liquid, ΔS° is very negative for this reaction.
B Substituting the advisable quantities into Equation \(\ref{Eq5}\),
\[\begin{marshal}\Delta G^\circ=\Delta H^\circ -T\Delta Southward^\circ &=-187.78\textrm{ kJ/mol}-(\textrm{298.xv Yard}) [-226.three\;\mathrm{J/(mol\cdot K)}\times\textrm{1 kJ/one thousand J}] \nonumber \\ &=-187.78\textrm{ kJ/mol}+67.47\textrm{ kJ/mol}=-120.31\textrm{ kJ/mol} \nonumber \end{marshal}\]
The negative value of ΔG° indicates that the reaction is spontaneous equally written. Because ΔS° and ΔH° for this reaction have the aforementioned sign, the sign of ΔG° depends on the relative magnitudes of the ΔH° and TΔS° terms. In this item instance, the enthalpy term dominates, indicating that the forcefulness of the bonds formed in the product more than compensates for the unfavorable ΔS° term and for the energy needed to break bonds in the reactants.
Practise \(\PageIndex{iii}\)
Calculate the standard free-energy modify (ΔG°) at 25°C for the reaction
\[2H_2(grand)+N_2(thousand) \rightleftharpoons N_2H_4(50) \nonumber \]
. At 25°C, the standard enthalpy modify (ΔH°) is fifty.vi kJ/mol, and the absolute entropies of the products and reactants are Southward°(NtwoH4) = 121.ii J/(mol•Yard), South°(N2) = 191.6 J/(mol•K), and S°(Htwo) = 130.7 J/(mol•Grand). Is the reaction spontaneous as written?
Answer:
Video Solution
149.five kJ/mol; no
Tabulated values of standard free energies of formation allow chemists to summate the values of ΔG° for a broad variety of chemical reactions rather than having to measure them in the laboratory. The standard free energy of germination (\(ΔG^∘_f\))of a compound is the alter in free energy that occurs when 1 mol of a substance in its standard state is formed from the component elements in their standard states. By definition, the standard costless energy of germination of an chemical element in its standard state is nix at 298.15 K. I mole of Cltwo gas at 298.15 M, for example, has \(ΔG^∘_f = 0\). The standard free energy of formation of a compound can be calculated from the standard enthalpy of germination (ΔH∘ f) and the standard entropy of formation (ΔS∘ f) using the definition of free energy:
\[Δ^o_{f} =ΔH^o_{f} −TΔS^o_{f} \characterization{Eq6}\]
Using standard costless energies of formation to calculate the standard complimentary energy of a reaction is analogous to calculating standard enthalpy changes from standard enthalpies of germination using the familiar "products minus reactants" rule:
\[ΔG^o_{rxn}=\sum mΔG^o_{f} (products)− \sum nΔ^o_{f} (reactants) \label{Eq7a}\]
where m and northward are the stoichiometric coefficients of each product and reactant in the counterbalanced chemic equation. A very large negative ΔG° indicates a stiff tendency for products to grade spontaneously from reactants; it does not, notwithstanding, necessarily bespeak that the reaction will occur rapidly. To brand this determination, we need to evaluate the kinetics of the reaction.
Example \(\PageIndex{4}\)
Calculate ΔG° for the reaction of isooctane with oxygen gas to give carbon dioxide and water (described in Instance 7). Use the following data:
- ΔG°f(isooctane) = −353.ii kJ/mol,
- ΔG°f(CO2) = −394.4 kJ/mol, and
- ΔG°f(H2O) = −237.ane kJ/mol. Is the reaction spontaneous equally written?
Given: balanced chemic equation and values of ΔG°f for isooctane, CO2, and H2O
Asked for: spontaneity of reaction as written
Strategy:
Use the "products minus reactants" dominion to obtain ΔG∘ rxn, remembering that ΔG°f for an chemical element in its standard state is zero. From the calculated value, determine whether the reaction is spontaneous as written.
Solution
The balanced chemical equation for the reaction is as follows:
\[\mathrm{C_8H_{eighteen}(l)}+\frac{25}{2}\mathrm{O_2(g)}\rightarrow\mathrm{8CO_2(1000)}+\mathrm{9H_2O(fifty)} \nonumber\]
We are given ΔG∘ f values for all the products and reactants except O2(yard). Because oxygen gas is an element in its standard country, ΔG∘ f (O2) is nothing. Using the "products minus reactants" rule,
\(\begin{align} \Delta 1000^\circ &=[8\Delta G^\circ_\textrm f(\mathrm{CO_2})+nine\Delta G^\circ_\textrm f(\mathrm{H_2O})]-\left[one\Delta G^\circ_\textrm f(\mathrm{C_8H_{eighteen}})+\dfrac{25}{2}\Delta G^\circ_\textrm f(\mathrm{O_2})\right]
\nonumber \\ &=[(\textrm{viii mol})(-394.4\textrm{ kJ/mol})+(\textrm{9 mol})(-237.1\textrm{ kJ/mol})]
\nonumber\\&-\left [(\textrm{1 mol})(-353.two\textrm{ kJ/mol})+\left(\dfrac{25}{2}\;\textrm{mol}\correct)(0 \textrm{ kJ/mol}) \right ]
\nonumber \\ &=-4935.9\textrm{ kJ }(\textrm{per mol of }\mathrm{C_8H_{18}}) \nonumber \end{align}\)
Because ΔG° is a large negative number, there is a strong tendency for the spontaneous formation of products from reactants (though non necessarily at a rapid rate). Also notice that the magnitude of ΔG° is largely determined by the ΔG∘ f of the stable products: water and carbon dioxide.
Exercise \(\PageIndex{4}\)
Calculate ΔG° for the reaction of benzene with hydrogen gas to give cyclohexane using the following information
- ΔG∘ f(benzene) = 124.five kJ/mol
- ΔG∘ f (cyclohexane) = 217.3 kJ/mol.
Is the reaction spontaneous as written?
Respond:
- 92.8 kJ; no
Video Solution
Calculated values of ΔG° are extremely useful in predicting whether a reaction will occur spontaneously if the reactants and products are mixed under standard conditions. We should note, however, that very few reactions are actually carried out under standard conditions, and calculated values of ΔG° may not tell us whether a given reaction will occur spontaneously under nonstandard conditions. What determines whether a reaction will occur spontaneously is the complimentary-energy change (ΔG) under the actual experimental weather, which are usually dissimilar from ΔG°. If the ΔH and TΔS terms for a reaction have the aforementioned sign, for example, so it may be possible to opposite the sign of ΔG by changing the temperature, thereby converting a reaction that is non thermodynamically spontaneous, having Keq < 1, to 1 that is, having a Keq > 1, or vice versa. Because ΔH and ΔS usually exercise not vary greatly with temperature in the absence of a phase modify, we tin use tabulated values of ΔH° and ΔS° to calculate ΔG° at various temperatures, equally long every bit no stage change occurs over the temperature range being considered.
Note
In the absence of a phase modify, neither \(ΔH\) nor \(ΔS\) vary greatly with temperature.
Instance \(\PageIndex{5}\)
Summate (a) ΔG° and (b) ΔG300 °C for the reaction N2(thousand)+3H2(g)⇌2NHiii(g), assuming that ΔH and ΔS practise not change betwixt 25°C and 300°C. Apply these data:
- Due south°(Due northii) = 191.half dozen J/(mol•Grand),
- S°(Htwo) = 130.7 J/(mol•Chiliad),
- Southward°(NHiii) = 192.viii J/(mol•K), and
- ΔH∘ f (NHiii) = −45.9 kJ/mol.
Given: balanced chemic equation, temperatures, S° values, and ΔH∘ f for NH3
Asked for: ΔG° and ΔG at 300°C
Strategy:
- Convert each temperature to kelvins. So calculate ΔS° for the reaction. Calculate ΔH° for the reaction, recalling that ΔH∘ f for whatever element in its standard state is zero.
- Substitute the appropriate values into Equation \(\ref{Eq5}\) to obtain ΔG° for the reaction.
- Bold that ΔH and ΔS are independent of temperature, substitute values into Equation \(\ref{Eq2}\) to obtain ΔG for the reaction at 300°C.
Solution
A To calculate ΔG° for the reaction using Equation \(\ref{Eq5}\), nosotros must know the temperature equally well equally the values of ΔS° and ΔH°. At standard conditions, the temperature is 25°C, or 298 One thousand. We can calculate ΔS° for the reaction from the absolute molar entropy values given for the reactants and the products using the "products minus reactants" rule:
\[\begin{align}\Delta S^\circ_{\textrm{rxn}}&=2S^\circ(\mathrm{NH_3})-[S^\circ(\mathrm{N_2})+3S^\circ(\mathrm{H_2})]
\nonumber\\ &=[\textrm{2 mol NH}_3\times192.8\;\mathrm{J/(mol\cdot Thousand)}]
\nonumber\\ &-\left \{[\textrm{one mol Due north}_2\times191.6\;\mathrm{J/(mol\cdot K)}]+[\textrm{3 mol H}_2\times130.7\;\mathrm{J/(mol\cdot K)}]\correct \} \nonumber\\ &=-198.i\textrm{ J/K (per mole of N}_2)\terminate{align} \nonumber\]
Nosotros can also calculate ΔH° for the reaction using the "products minus reactants" rule. The value of ΔH∘ f (NH3) is given, and ΔH∘ f is nil for both N2 and H2:
\[\brainstorm{align}\Delta H^\circ_{\textrm{rxn}}&=2\Delta H^\circ_\textrm f(\mathrm{NH_3})-[\Delta H^\circ_\textrm f(\mathrm{N_2})+3\Delta H^\circ_\textrm f(\mathrm{H_2})] \nonumber \\ &=[2\times(-45.9\textrm{ kJ/mol})]-[(1\times0\textrm{ kJ/mol})+(three\times0 \textrm{ kJ/mol})] \nonumber \\ &=-91.8\textrm{ kJ(per mole of N}_2) \nonumber\end{marshal} \nonumber\]
B Inserting the appropriate values into Equation \(\ref{Eq5}\)
\[\Delta One thousand^\circ_{\textrm{rxn}}=\Delta H^\circ-T\Delta South^\circ=(-\textrm{91.8 kJ})-(\textrm{298 K})(-\textrm{198.one J/1000})(\textrm{i kJ/1000 J})=-\textrm{32.7 kJ (per mole of N}_2) \nonumber\]
C To calculate ΔG for this reaction at 300°C, we assume that ΔH and ΔS are independent of temperature (i.e., ΔH300°C = H° and ΔS300°C = ΔS°) and insert the appropriate temperature (573 K) into Equation \(\ref{Eq2}\):
\[\begin{align}\Delta G_{300^\circ\textrm C}&=\Delta H_{300^\circ\textrm C}-(\textrm{573 K})(\Delta S_{300^\circ\textrm C})=\Delta H^\circ -(\textrm{573 Yard})\Delta Due south^\circ \nonumber \\ &=(-\textrm{91.8 kJ})-(\textrm{573 M})(-\textrm{198.1 J/K})(\textrm{1 kJ/m J})=21.vii\textrm{ kJ (per mole of N}_2) \nonumber \stop{align} \nonumber \]
In this example, irresolute the temperature has a major effect on the thermodynamic spontaneity of the reaction. Under standard conditions, the reaction of nitrogen and hydrogen gas to produce ammonia is thermodynamically spontaneous, but in practice, it is too wearisome to be useful industrially. Increasing the temperature in an effort to brand this reaction occur more rapidly besides changes the thermodynamics by causing the −TΔS° term to dominate, and the reaction is no longer spontaneous at high temperatures; that is, its Keq is less than one. This is a classic example of the conflict encountered in real systems between thermodynamics and kinetics, which is often unavoidable.
Exercise \(\PageIndex{5}\)
Summate
- \(ΔG°\) and
- \(ΔG_{750°C}\)
for the following reaction
\[2NO_{(chiliad)}+O_{2\; (g)} \rightleftharpoons 2NO_{2\; (1000)} \nonumber\]
which is important in the formation of urban smog. Presume that \(ΔH\) and \(ΔS\) do not change betwixt 25.0°C and 750°C and utilise these data:
- S°(NO) = 210.viii J/(mol•K),
- S°(O2) = 205.two J/(mol•Chiliad),
- S°(NO2) = 240.i J/(mol•K),
- ΔH∘ f(NO2) = 33.2 kJ/mol, and
- ΔH∘ f (NO) = 91.three kJ/mol.
Respond
- −72.five kJ/mol of \(O_2\)
- 33.8 kJ/mol of \(O_2\)
Video Solution
The issue of temperature on the spontaneity of a reaction, which is an important cistron in the design of an experiment or an industrial process, depends on the sign and magnitude of both ΔH° and ΔS°. The temperature at which a given reaction is at equilibrium tin can be calculated by setting ΔG° = 0 in Equation \(\ref{Eq5}\), every bit illustrated in Example \(\PageIndex{iv}\).
Instance \(\PageIndex{6}\)
The reaction of nitrogen and hydrogen gas to produce ammonia is one in which ΔH° and ΔS° are both negative. Such reactions are predicted to be thermodynamically spontaneous at depression temperatures simply nonspontaneous at high temperatures. Use the information in Example \(\PageIndex{3}\) to calculate the temperature at which this reaction changes from spontaneous to nonspontaneous, assuming that ΔH° and ΔS° are independent of temperature.
Given: ΔH° and ΔS°
Asked for: temperature at which reaction changes from spontaneous to nonspontaneous
Strategy:
Set ΔG° equal to cipher in Equation \(\ref{Eq5}\) and solve for T, the temperature at which the reaction becomes nonspontaneous.
Solution
In Example \(\PageIndex{3}\), we calculated that ΔH° is −91.8 kJ/mol of Nii and ΔS° is −198.1 J/K per mole of N2, corresponding to ΔG° = −32.7 kJ/mol of N2 at 25°C. Thus the reaction is indeed spontaneous at low temperatures, as expected based on the signs of ΔH° and ΔS°. The temperature at which the reaction becomes nonspontaneous is found past setting ΔG° equal to zero and rearranging Equation \(\ref{Eq5}\) to solve for T:
\[\begin{align}\Delta G^\circ &=\Delta H^\circ - T\Delta South^\circ=0
\\ \Delta H^\circ &=T\Delta Due south^\circ
\\ T=\dfrac{\Delta H^\circ}{\Delta S^\circ}&=\dfrac{(-\textrm{91.eight kJ})(\textrm{chiliad J/kJ})}{-\textrm{198.ane J/K}}=\textrm{463 K}\end{align}\]
This is a example in which a chemical engineer is severely limited by thermodynamics. Any attempt to increment the charge per unit of reaction of nitrogen with hydrogen by increasing the temperature volition cause reactants to exist favored over products above 463 K.
Exercise \(\PageIndex{6}\)
ΔH° and ΔS° are both negative for the reaction of nitric oxide and oxygen to course nitrogen dioxide. Use those data to summate the temperature at which this reaction changes from spontaneous to nonspontaneous.
Reply: 792.six K
Summary
- The change in Gibbs complimentary energy, which is based solely on changes in state functions, is the benchmark for predicting the spontaneity of a reaction.
We can predict whether a reaction will occur spontaneously by combining the entropy, enthalpy, and temperature of a arrangement in a new state function called Gibbs free energy (G). The alter in complimentary free energy (ΔG) is the divergence betwixt the heat released during a process and the heat released for the same process occurring in a reversible fashion. If a organisation is at equilibrium, ΔG = 0. If the procedure is spontaneous, ΔG < 0. If the process is not spontaneous as written merely is spontaneous in the reverse direction, ΔG > 0. At constant temperature and pressure, ΔG is equal to the maximum corporeality of work a organization tin can perform on its surround while undergoing a spontaneous modify. The standard complimentary-free energy change (ΔG°) is the change in free energy when one substance or a set of substances in their standard states is converted to one or more than other substances, besides in their standard states. The standard gratuitous energy of formation (ΔG∘ f), is the change in free free energy that occurs when ane mol of a substance in its standard state is formed from the component elements in their standard states. Tabulated values of standard free energies of formation are used to calculate ΔG° for a reaction.
Which Reaction Would Cause An Increase In Entropy,
Source: https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_General_Chemistry_(Petrucci_et_al.)/19%3A_Spontaneous_Change%3A_Entropy_and_Gibbs_Energy/19.6%3A_Gibbs_Energy_Change_and_Equilibrium
Posted by: faucettconwhod.blogspot.com


0 Response to "Which Reaction Would Cause An Increase In Entropy"
Post a Comment